
前言
文章中所有排序算法默认非递减。
1. 直接插入排序
-
算法介绍
直接插入排序,属于插入类排序,该算法稳定,顾名思义,每次都会将一个待排元素直接插入到有序序列中,打个比方,有一个序列是
2, 5, 4, 6, 3- 第一次排序:只有 2 一个元素,所以无需排序。排序结果为 2。
- 第二次排序:待排元素为 5,5 比 2 大,所以不需要移动元素。排序结果为 2, 5。
- 第三次排序:待排元素为 4,4 比 5 小,所以 5 向后移动一位;而 4 比 2 大,所以 4 应该插入 2 的后面,5 的前面。排序结果为 2, 4, 5。
- 第四次排序:待排元素为 6,6 比 5 大,所以直接插入到 5 的后面即可。排序结果为 2, 4, 5, 6。
- 第五次排序:待排元素为 3,3 比 6 小,6 向后移动一位;继续和 5 , 4 依次比较,由于 3 比 5 和 4 都要小,5 , 4 也依次向后移动一位;直到 3 比 2 大,所以 3 插入到 2 的后面,4 的前面。排序结果为 2 , 3 , 4 , 5 , 6。
-
具体代码
def insert_sort_directly(arr): """ 直接插入排序 :param arr: 列表 :return: arr """ n = len(arr) for i in range(1, n): # 从第二个元素开始遍历 temp = arr[i] # 保存待插入元素 j = i - 1 # 右边扫描开始下标 while j >= 0 and temp < arr[j]: # 从右向左扫描,直到找到比 temp 小的元素,将比 temp 大的元素依次右移一位 arr[j + 1] = arr[j] j -= 1 arr[j + 1] = temp # 找到插入位置,将 temp 插入 return arr
2. 希尔排序
-
算法介绍
希尔排序属于插入类排序,且该排序不稳定,又称作缩小增量排序,是直接插入排序的优化版。
希尔排序是对下标按照一定增量进行分组,对每组数据进行直接插入排序;随着增量减少,每组关键字越来越多,直到增量为 1,整个数据恰好被分成一组,排序结束。
例如,初始序列为:
2, 5, 4, 6, 3取初始增量 5 / 2 = 2,其中 5 为序列的总个数,由于增量只能为整数,所以需要取整。
那么,
2, 4, 3一组,5, 6为一组。2 的下标为 0,4 的下标为 2,3 的下标为 4,以增量 2 为间隔依次取组。
对
2, 4, 3进行直接插入排序,排序结果为2, 3, 4;对5, 6进行直接插入排序,排序结果为5, 6。得到总序列排序结果
2, 5, 3, 6, 4。开始缩小增量,增量为原来增量 / 2,即 2 / 2 = 1。再继续对待排序列进行分组,由于增量为 1,只有一组数据:
2, 5, 3, 6, 4,对该数据执行直接插入排序,得到最终排序结果:2, 3, 4, 5, 6 -
具体代码
def shell_sort(arr): """ 希尔排序 :param arr: 列表 """ n = len(arr) # 列表长度 step = n // 2 # 步长,初始值为列表长度除 2 取整 while step > 0: for j in range(step, n): # 从下标 step 遍历到 n - 1 while j - step >= 0 and arr[j] < arr[j - step]: # 比较下标相差 step 的两个元素,若 j- step 比 j 对应元素大,将两者交换 arr[j], arr[j - step] = arr[j - step], arr[j] j -= step step = step // 2 # 步长减半
3. 冒泡排序
-
算法介绍
冒泡排序又称起泡排序,属于交换类排序,该算法稳定。
冒泡排序从第一个元素开始,比较当前元素和下一个元素,若当前元素大于下一个元素,将两者交换,依次对所有元素进行比较,那么经过一次冒泡排序,最大的数像石头一样沉入底部,小的数像气泡一样冒出。
例如,有一个待排序列:
2, 4, 5, 3, 6-
比较 2 和 4 ,2 小于 4,无需交换。
-
比较 4 和 5,无需交换。
-
比较 5 和 3 ,由于 5 比 3 大,将两者交换,得到序列:
2, 4, 3, 5, 6 -
比较 5 和 6,无需交换。
2, 4, 3, 5, 6可以看到,经过一次冒泡排序,最大元素 6 被交换到了最右端。接下来,只需要对剩下的 n - 1 个元素
2, 4, 5, 3进行冒泡排序即可,依次类推,直到没有发生元素交换,排序结束。
-
-
具体代码
def bubble_sort(arr): """ 冒泡排序(起泡排序) :param arr: 列表 :return: arr """ n = len(arr) for i in range(n - 1, 0, -1): # 反向遍历下标从 n - 1 到 1 的元素 flag = 0 # 标记是否发生元素交换 for j in range(0, i): # 遍历下标 0 ~ i - 1 的元素 if arr[j] > arr[j + 1]: # 若当前元素大于下一个元素,将两者交换 arr[j], arr[j + 1] = arr[j + 1], arr[j] flag = 1 # 标记已发生交换 if flag == 0: # 未发生交换,结束排序 return arr
4. 快速排序
-
算法介绍
快速排序是一种交换类排序,且该算法不稳定。
基本思想:选定一个基准元素,根据基准将待排序列划分为两部分,左边部分元素小于基准,右边部分元素大于基准。接下来对左边和右边部分继续进行快排,直到整个序列有序为止,整个排序过程是递归进行的。
话不多说,直接上大佬画的图。
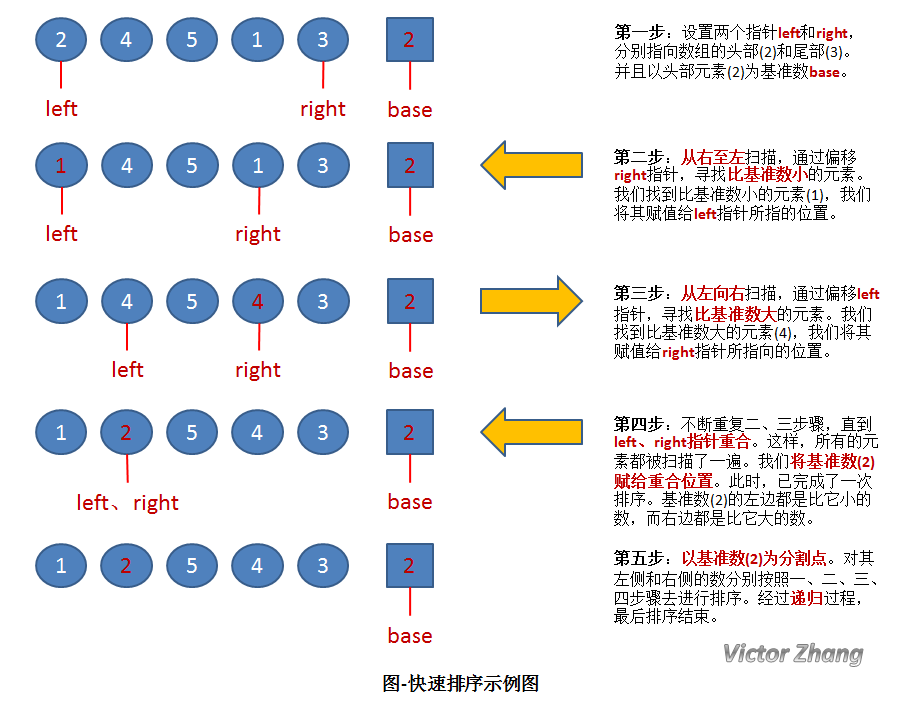
-
具体代码
def quick_sort(arr, left, right): """ 快速排序 :param arr: 列表 :param left: 开始下标 :param right: 结束下标 """ i, j = left, right # i 为左指针,j 为右指针 if left < right: # 递归出口条件 base = arr[left] # base 记录基准值 while i < j: # 对子列进行快排,当两个指针相遇时,结束循环 while i < j and arr[j] >= base: # 从右往左扫描,直到找到比 base 小的值 j -= 1 if i < j: # 右指针在左指针右边,才能进行赋值操作(因为可能会出现未找到比基准元素小的情况,而此时 j <= i) arr[i] = arr[j] # 把右指针对应的值赋给左指针 while i < j and arr[i] <= base: # 从左向右扫描,直到找到比 base 大的值 i += 1 if i < j: arr[j] = arr[i] # 把左指针对应的值赋给右指针 arr[i] = base # 基准值插入到最终位置(此时左右指针相遇) quick_sort(arr, left, i - 1) # 对左子列(基准值左边部分)进行快排 quick_sort(arr, i + 1, right) # 对右子列(基准值右边部分)进行快排
5. 堆排序
-
基本概念
完全二叉树:一颗二叉树有 k 层,除第 k 层之外,其他层结点都达到最大数,且第 k 层所有节点都连续集中在最左边。
堆是一颗完全二叉树,且每个结点值都大于等于左右孩子结点值(大顶堆)或每个结点的值都小于等于左右孩子结点值(小顶堆)。如下所示:
-
算法介绍
堆排序是基于堆设计的一种选择排序算法,且算法不稳定。
本文中,堆排序的数组下标从 0 开始计数。对于大顶堆来说,满足数组下标定义:
arr[i] >= arr[2 * i + 1] and arr[i] >= arr[2 * i + 2]例如有一个待排序列:
4, 6, 8, 5, 9先将其转换为完全二叉树:
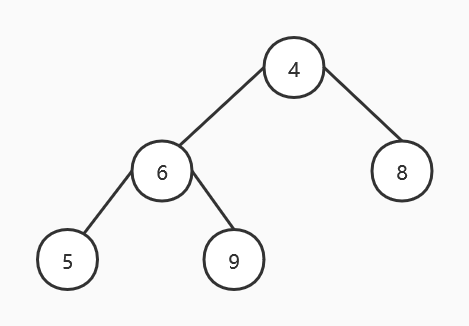
再将其调整为大顶堆,从右往左,从上往下依次检查所有的非叶子节点,进行调整。
第一次调整,从 6 开始调整:
由于 6 小于右孩子 9,将其与右孩子交换:
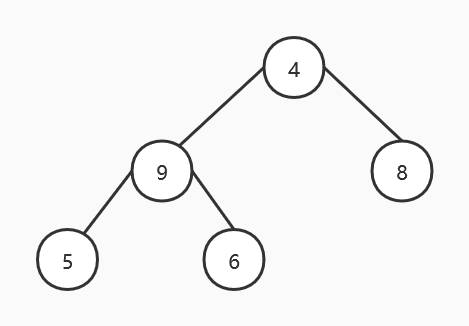
然后调整 4,由于 4 比左孩子 9 和右孩子 8 都要小,于是将 4 和左孩子交换(如果 4 和右孩子交换,仍然不满足大顶堆的定义,还需进行调整),得到如下结果:
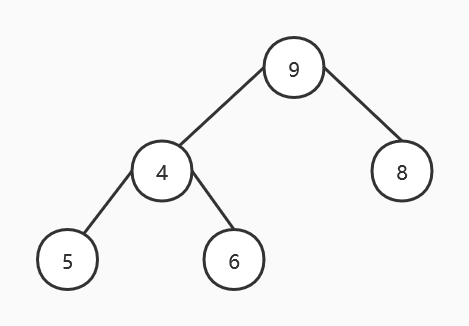
再对 4 进行调整,4 小于左孩子 5 和右孩子 6,因此将 4 与右孩子交换,得到如下结果:
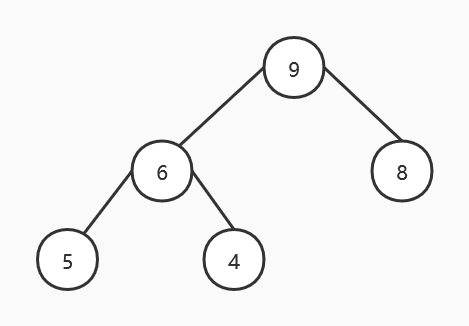
经过若干次调整,该完全二叉树已经满足大顶堆定义,接下来只需交换根结点 9 与底层最右边结点 4 的值即可。得到第一次堆排序结果:
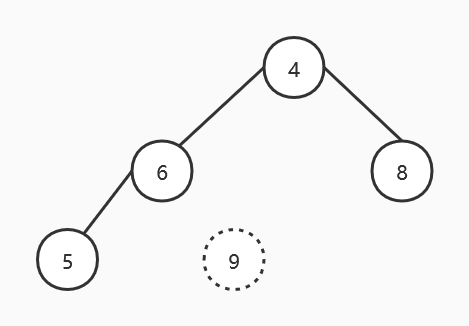
经过第一次堆排序(调整大顶堆 + 交换),最大值 9 已经加入到有序序列中,接下来只要对剩下的二叉树继续进行堆排序(调整大顶堆 + 交换)即可,直到所有序列均有序。
总结一下堆排序的核心算法流程:
- 将待排序列调整为大顶堆。
- 交换根结点元素(最大值)和末尾元素(二叉树底层最右边元素),有序序列增加一个,无序序列减少一个,继续对剩下的无序序列进行堆排序(调整大顶堆 + 交换根结点与末尾元素),以此类推,直到只剩下一个元素为止。
-
具体代码
注意:这里的二叉树用数组保存,且下标从 0 开始计算。
def adjust(arr, parent, n): """ 调整二叉树 :param arr: 列表 :param parent: 父节点下标 :param n: 列表长度 """ temp = arr[parent] # 保存父结点的值 child = 2 * parent + 1 # child 指向左孩子 while child < n: if child + 1 < n and arr[child] < arr[child + 1]: # 若右孩子存在且大于左孩子,将 child 指向右孩子 child += 1 if temp > arr[child]: # 父结点已大于左右孩子,结束循环 break arr[parent] = arr[child] # 把孩子结点的值赋给父结点 parent = child # 选取孩子结点的左孩子,继续进行调整 child = 2 * parent + 1 arr[parent] = temp def heap_sort(arr): """ 堆排序 :param arr: 列表 """ length = len(arr) # 循环建立初始大顶堆 for i in range((length - 1) // 2, -1, -1): adjust(arr, i, length) # n - 1 次循环,完成堆排序 for j in range(length - 1, 0, -1): arr[0], arr[j] = arr[j], arr[0] # 交换第一个元素和最后一个元素 adjust(arr, 0, j) # 对剩余的 j - 1 个元素进行调整
6. 简单选择排序
-
算法介绍
简单选择排序属于选择类排序,且算法不稳定。
-
基本思想:每次从待排序列中找出最小元素,将其放在有序序列末尾,直到待排序列有序。
-
具体流程:
例如有一个待排序列:
2, 5, 4, 6, 3-
第一趟排序:2 为序列
2, 5, 4, 6, 3中最小值,无需变动:2, 5, 4, 6, 3 -
第二趟排序:剩余序列
5, 4, 6, 3中最小值为 3,交换 5 和 3 ,得到序列:2, 3, 4, 6, 5 -
第三趟排序:剩余序列
4, 6, 5中最小值为 4,无需变动:2, 3, 4, 6, 5 -
第四趟排序:剩余序列
6, 5中最小值为 5,交换 6 和 5,得到序列:2, 3, 4, 5, 6
-
-
-
具体代码
def simple_sort(arr): """ 简单选择排序 :param arr: 列表 """ n = len(arr) for i in range(n - 1): # 经过 n - 1 次遍历后,已经全部有序 index = i # 保存最小值下标 for j in range(i + 1, n): if arr[j] < arr[index]: # 若找到比当前最小值 arr[index] 还要小的元素,更新最小值下标 index = j arr[i], arr[index] = arr[index], arr[i] # 将最小值和待排序列第一个元素交换
7. 归并排序
-
算法介绍
归并排序是一种稳定的排序算法,核心思想是归并,采用分治策略来解决问题。
话不多说,直接上图(从大佬那边偷来的? )。
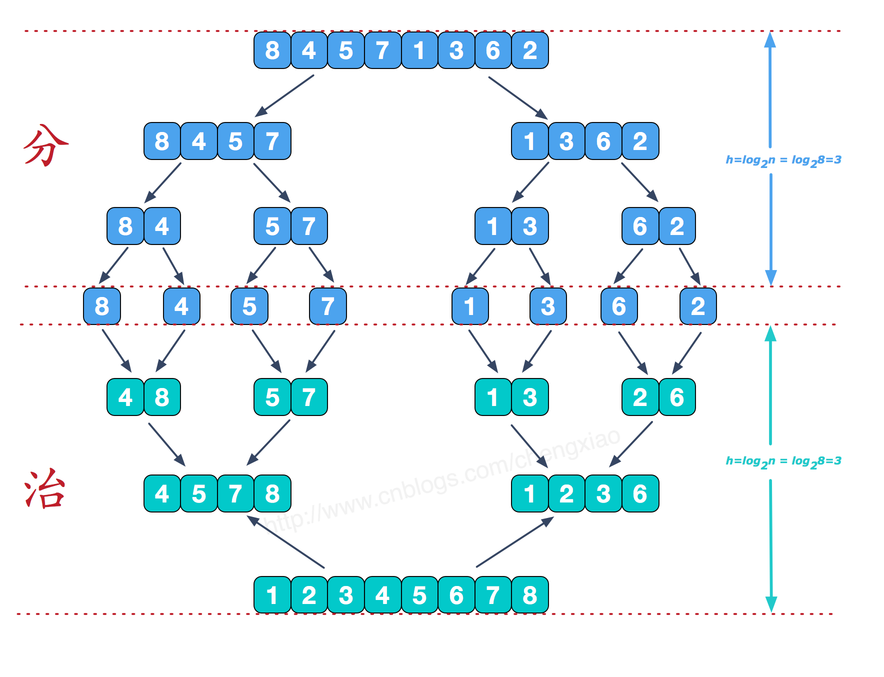
-
具体代码
def merge(left_arr, right_arr): """ 合并两个列表(非递减) :param left_arr: 左列表 :param right_arr:右列表 :return: 合并后的列表 """ result = [] i, j = 0, 0 while i < len(left_arr) and j < len(right_arr): # 双指针遍历两个列表,将两个列表合并 if left_arr[i] < right_arr[j]: # 若 i 指向元素小于 j 指向元素,将 left_arr[i] 插入 result 中 result.append(left_arr[i]) i += 1 # i 向右移动一位 else: result.append(right_arr[j]) j += 1 while i < len(left_arr): # 将剩余元素依次写入 result 中 result.append(left_arr[i]) i += 1 while j < len(right_arr): result.append(right_arr[j]) j += 1 return result def merge_sort(arr): """ 归并排序 :param arr: 列表 :return:列表 """ n = len(arr) if n <= 1: # 若长度小于等于 1,结束排序(递归出口) return arr mid = n // 2 left_arr = merge_sort(arr[:mid]) # 对左列表进行归并排序 right_arr = merge_sort(arr[mid:]) # 对右列表进行归并排序 return merge(left_arr, right_arr) # 合并左右两个列表
8. 基数排序
-
算法介绍
基数排序和其他排序不同,无需比较关键字的大小,而是从低到高根据位数进行划分和排序,且该算法稳定。
阿拉伯数字的每一位都由
0 ~ 9组成,例如50,它的个位数是0,十位数是5。例如,有一个待排序列:
73 22 93 43 55 14 28 65 39 81先根据个位数将这些数划分,如下所示:
81 的个位数是 1,因此将其放到 1 对应的那一栏中。
0 1 81 2 22 3 73 93 43 4 14 5 55 65 6 7 8 28 9 39 然后,根据上述表格中个位数
0 ~ 9的顺序,得到如下排序结果:81, 22, 73, 93, 43, 14, 55, 65, 28, 39经过一次排序,待排元素的个位数已经有序。接下来,依次对百位数、千位数、... 进行排序,最终得到有序序列。
-
具体代码
def radix_sort(arr): """ 基数排序 :param arr: 列表 """ curr_digit = 0 # 记录当前位数是第几位,0 表示个位,1表示十位,依次类推 max_val = max(arr) # 获取列表中的最大值 max_digit = len(str(max_val)) # 记录最大值的位数总数 while curr_digit < max_digit: # 注意循环条件:最大位数是 max_digit - 1 bucket_list = [[] for _ in range(10)] # 建立二维空数组,用于保存数据 for i in arr: digit = (i // (10 ** curr_digit)) % 10 # 计算当前位数上的数字 bucket_list[digit].append(i) # 将当前元素写入二维数组中 del arr[:] # 清空列表 for j in bucket_list: # 将排序好的元素写入原列表 arr for k in j: arr.append(k) curr_digit += 1 # 位数 + 1
常见算法时间复杂度,空间复杂度和稳定性
| 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 | |
|---|---|---|---|---|---|
| 直接插入排序 | O ( n^2 ) | O ( n ) | O ( n^2 ) | O ( 1 ) | 稳定 |
| 折半插入排序 | O ( n^2 ) | O ( nlogn ) | O ( n^2 ) | O ( 1 ) | 稳定 |
| 希尔排序 | O ( n^1.3 ) | O ( n ) | O ( n^2 ) | O ( 1 ) | 不稳定 |
| 冒泡排序 | O ( n^2 ) | O ( n ) | O ( n^2 ) | O ( 1 ) | 稳定 |
| 快速排序 | O ( nlogn ) | O ( nlogn ) | O ( n^2 ) | O ( nlogn ) | 不稳定 |
| 简单选择排序 | O ( n^2 ) | O ( n ) | O ( n^2 ) | O ( 1 ) | 不稳定 |
| 堆排序 | O ( nlogn ) | O ( nlogn ) | O ( nlogn ) | O ( 1 ) | 不稳定 |
| 二路归并排序 | O ( nlogn ) | O ( nlogn ) | O ( nlogn ) | O ( n ) | 稳定 |
| 基数排序 | O ( d(n + r) ) | O ( d(n + rd) ) | O ( d(n + r) ) | O ( n + rd ) | 稳定 |



