在神经网络中加入非线性的激活函数可以使其具备分层的非线性映射学习能力。
Sigmoid 函数
Sigmoid 激活函数的公式为：
Sigmoid(x)=\frac{1}{1+e^{-x}}
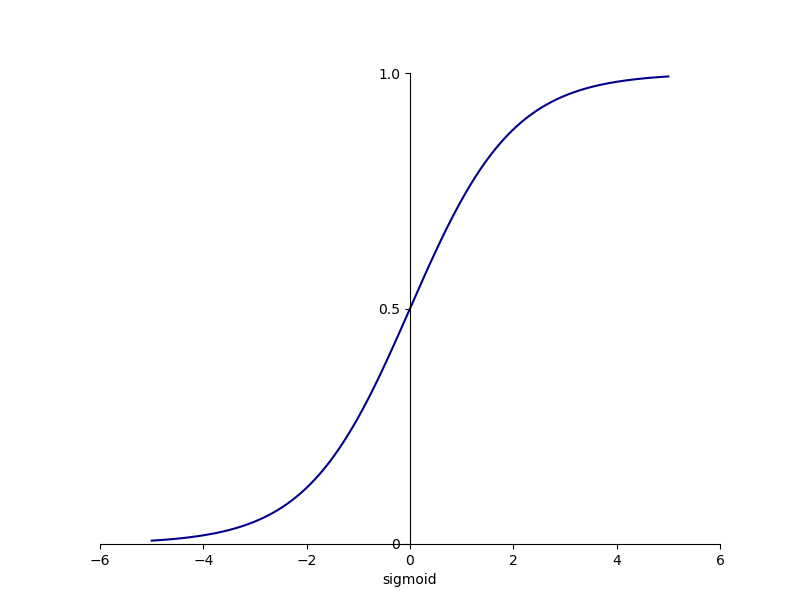
Sigmoid 函数可以将一个实数映射到 (0, 1) 范围内，可以用在 LSTM（Long Short-Term Memory，长短期记忆）中的各种门上，模拟门的关闭和开启状态。此外，Sigmoid 函数可以用来表示概率，还可以用于输入的归一化处理。Sigmoid 函数的图像如下所示：
Tanh 函数
Tanh 激活函数也是常见的激活函数，它可以将一个实数映射到 (-1, 1) 之间，其示意图如下所示：
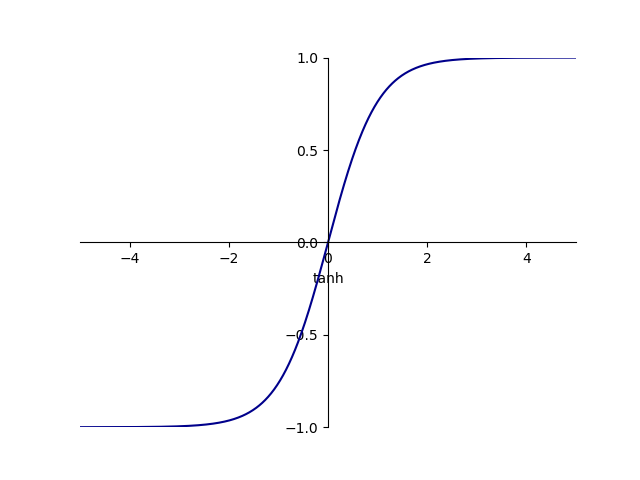
Tanh 函数的取值可以是负值，在某些需要抑制神经元的场景时，需要利用到该特性。例如，在 LSTM 中，可以利用 Tanh 函数的负值区来模拟“遗忘”。
Tanh 函数的公式为：
Tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2Sigmoid(2x)-1
由上述公式可知 Tanh 函数和 Sigmoid 函数之间存在一定的线性关系，两者形状类似，只是尺度和范围不同。因此，Tanh 函数和 Sigmoid 函数存在同样的缺陷——梯度弥散（Gradient Vanishing），导致训练效率不高。因此，如何防止神经网络陷入梯度弥散（如何提升网络的训练效率）是深度学习领域的热门研究话题。
目前在神经网络中，最常用的激活函数是修正线性单元 ReLU（Rectified Linear Unit）。
ReLU 函数
标准的 ReLU 函数很简单，它的函数形式为：
f(x)=max(x, 0)
为了让它在原点处光滑可导，Softplus 函数被提出来了，它的函数形式为：
f(x)=ln(1+e^x)
Softplus 函数是对 ReLU 函数平滑逼近的解析形式，且它的导数恰好为 Sigmoid 函数。标准 ReLU 函数和 Softplus 函数的图像如下所示：
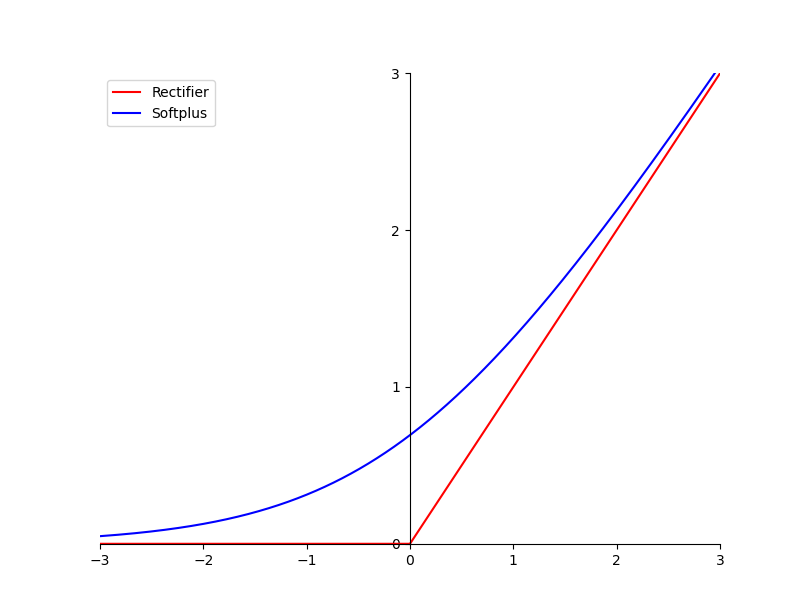
和 Sigmoid 激活函数相比，ReLU 函数的主要优点体现在以下三个方面：
- 单侧抑制。如上图所示，当输入值小于 0 时，神经元处于抑制状态；反之，神经元处于激活状态。而且 ReLU 函数求导比较简单，所以使用 ReLU 函数时随机梯度递减的收敛速度比 Sigmoid 和 Tanh 函数要快很多。
- 相对宽阔的兴奋边界。ReLU 函数在激活状态下的取值范围（当输入值大于 0 时的输出值范围）比 Sigmoid 和 Tanh 函数大得多。
- 稀疏激活。Sigmoid 函数将处于抑制状态的神经元设置了一个非常小的值，会增大计算负担。但 ReLU 函数将处于抑制状态的神经元的值直接设为 0，使得这些神经元不再参与后续的运算，增加了网络的稀疏性。
