苍茫误此生博客
搜索
教程

弗洛伊德算法

1484 次阅读约 8 分钟 · 2069 字
算法
弗洛伊德算法

基本概念

图

图在数据结构中可以表示一对多的关系，通常分为有向图和无向图。

  • 图是由顶点集 V 和顶点间的关系集合 E （边的集合）组成的一种数据结构。
  • 用二元组定义为：G = (V, E)

例如：

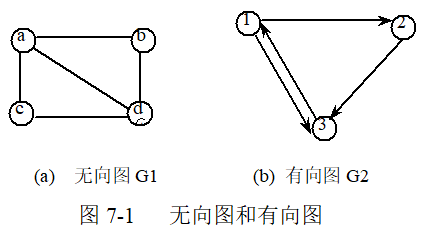
上图中，G1 为无向图，G2 为有向图。在 G2 中有箭头表示方向，称这样的图为有向图，否则为无向图。

G1 和 G2 的数据结构分别可以表示为：

在无向图中，边 (x, y) 和边 (y, x) 表示的结果相同（因为无向图是没有方向的），用圆括号表示。

在有向图中，边 <x, y> 和边 (y, x) 表示的结果不同，<x, y> 表示从顶点 x 到 y 存在边，x 为起点，y 为终点。

  • G1 = (V1, E1)，其中 V1 = {a, b, c, d}，E1 = {(a, b), (a, c), (a, d), (b, d), (c, d)}
  • G2 = (V2, E2)，其中 V2 = {1, 2, 3}，E2 = {<1, 2>, <1, 3>, <2, 3>, <3, 1>}

邻接矩阵

邻接矩阵是表示顶点之间相邻关系的矩阵。由于图的逻辑结构分为两部分，顶点和边，因此，用一个一维数组存放图中所有顶点数据，用一个二维数组存放边的数据（顶点之间的关系）。

弗洛伊德算法

弗洛伊德算法是用来求解有向网（带权有向图）中两个顶点之间的最短路径。

算法分析

弗洛伊德算法的核心思想是，依次将每个顶点作为中介顶点，然后判断由开始顶点经过此中介顶点，再由此中介顶点到结束顶点之间的路径之和是否比原路径短，若比原路径短，则更新对应的路径。

记 dis<vi, vj> 为顶点 vi 到 vj 的距离，若能找到一个中介顶点 vk，使得 dis<vi, vk> + dis<vk, vj> < dis<vi, vj>，则更新 dis<vi, vj> 的值为dis<vi, vk> + dis<vk, vj>。

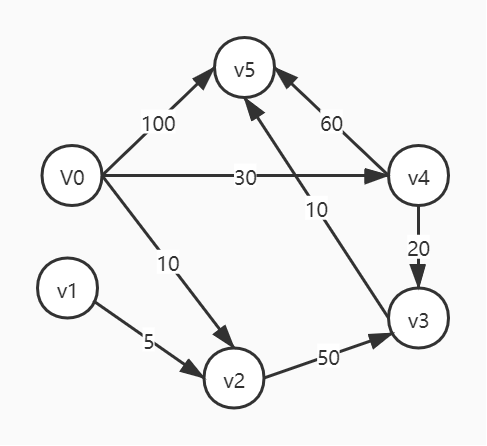
image20210425214252xqxnytq.png

以上有向网对应的邻接矩阵为：

注意：

  • 规定顶点到自身的距离为无穷大。
  • 邻接矩阵表示相邻顶点之间的关系，也就是说，如果两个顶点不能直接到达，则这两个顶点之间的距离为无穷大。
v0 v1 v2 v3 v4 v5
v0 $\infty$ $\infty$ 10 $\infty$ 30 100
v1 $\infty$ $\infty$ 5 $\infty$ $\infty$ $\infty$
v2 $\infty$ $\infty$ $\infty$ 50 $\infty$ $\infty$
v3 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ 10
v4 $\infty$ $\infty$ $\infty$ 20 $\infty$ 60
v5 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ $\infty$

先以 v0 为中介顶点，来更新上面的矩阵，矩阵保持不变（因为 v0 的入度为 0，不具备作中介顶点的条件）。

以 v1 为中介顶点，由于 v1 的入度为 0，同理，矩阵仍保持不变。

以 v2 为中介顶点，v0 到 v3 有一条新路径，从 v0 经过 v2 再到 v3，且 dis<v0, v2> + dis<v2, v3> 小于 dis<v0, v3>，因此将 dis<v0, v3> 更新为 60；同理，更新 dis<v1, v3>：

v0 v1 v2 v3 v4 v5
v0 $\infty$ $\infty$ 10 60 30 100
v1 $\infty$ $\infty$ 5 55 $\infty$ $\infty$
v2 $\infty$ $\infty$ $\infty$ 50 $\infty$ $\infty$
v3 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ 10
v4 $\infty$ $\infty$ $\infty$ 20 $\infty$ 60
v5 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ $\infty$

以 v3 为中介顶点，更新 dis<v0, v5>，dis<v1, v5>，dis<v2, v5>，dis<v4, v5>：

v0 v1 v2 v3 v4 v5
v0 $\infty$ $\infty$ 10 60 30 70
v1 $\infty$ $\infty$ 5 55 $\infty$ 65
v2 $\infty$ $\infty$ $\infty$ 50 $\infty$ 60
v3 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ 10
v4 $\infty$ $\infty$ $\infty$ 20 $\infty$ 30
v5 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ $\infty$

以 v4 为中介顶点，更新 dis<v0, v3> 和 dis<v0, v5>：

v0 v1 v2 v3 v4 v5
v0 $\infty$ $\infty$ 10 50 30 60
v1 $\infty$ $\infty$ 5 55 $\infty$ 65
v2 $\infty$ $\infty$ $\infty$ 50 $\infty$ 60
v3 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ 10
v4 $\infty$ $\infty$ $\infty$ 20 $\infty$ 30
v5 $\infty$ $\infty$ $\infty$ $\infty$ $\infty$ $\infty$

以 v5 为中介结点，由于 v5 出度为 0 ，以 v5 作为中介结点不会影响其他路径的距离，因此矩阵保持不变。

算法流程

  • 构建有向网
    • 输入顶点个数和弧边数；
    • 输入各顶点的值；
    • 初始化邻接矩阵的值，默认为无穷大；
    • 输入各个弧边的起始顶点，结束顶点以及边的权值。
  • 弗洛伊德算法
    • 初始化数组 P 和数组 D，数组 P 用来存储最短路径中经过的顶点的下标，数组 D 用来保存各个顶点之间的最短路径；
    • 遍历每一个顶点 K，将顶点 K 作为中介结点，计算从开始顶点 A 到到顶点 K，再从顶点 K 到结束顶点 B 的所有弧边权值之和是否小于顶点 A 到顶点 B 之间的距离，若小于，则修改顶点 A 到顶点 B 之间的距离为更小值。

代码实现

#include <iostream>
using namespace std;

#define MAX_VERTEX_NUM 30 // 最大顶点数
#define INFINITY 65535    // 表示无穷大

typedef int VRType;                                         // 弧的权值类型
typedef int VertexType;                                     // 图中顶点的数据类型
typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];     // 用于存储最短路径中经过的顶点下标
typedef int ShortPathTable[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 用于存储各个顶点之间的最短路径

class MGraph
{
private:
    VertexType vexs[MAX_VERTEX_NUM];             // 存储中顶点数据
    VRType arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 二维数组，记录顶点之间的关系（弧边的权值）
    int vexNum;                                  // 顶点数
    int arcNum;                                  // 弧边数

public:
    MGraph() {}
    int getVexNum() // 获取顶点数
    {
        return vexNum;
    }
    int getArcNum() // 获取弧边数
    {
        return arcNum;
    }
    int locateVex(MGraph G, VertexType v);                              // 根据顶点数据，找到顶点所在位置
    void createUDG(MGraph &G);                                          // 构造网
    void shortestPathFloyd(MGraph G, PathMatrix &P, ShortPathTable &D); // 弗洛伊德算法
};

// 根据顶点数据，找到顶点所在位置
int MGraph::locateVex(MGraph G, VertexType v)
{
    int i = 0;
    while (i < G.vexNum)
    {
        if (G.vexs[i] == v) // 找到位置，直接返回下标
        {
            return i;
        }
        i++;
    }
    return -1; // 未找到，返回 - 1
}

// 构造网
void MGraph::createUDG(MGraph &G)
{
    cout << "请输入顶点数：";
    cin >> G.vexNum;
    cout << "请输入弧边数：";
    cin >> G.arcNum;

    cout << "请输入各顶点的值：";
    for (int i = 0; i < G.vexNum; i++)
    {
        cin >> G.vexs[i];
    }

    // 初始化 G.arcs 数组，默认值为 INFINITY
    for (int i = 0; i < G.vexNum; i++)
    {
        for (int j = 0; j < G.vexNum; j++)
        {
            G.arcs[i][j] = INFINITY;
        }
    }

    cout << "请输入顶点数据和弧边权重：" << endl;
    for (int i = 0; i < G.arcNum; i++)
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        int n = locateVex(G, v1);
        int m = locateVex(G, v2);

        if (n == -1 || m == -1)
        {
            cout << "不存在该顶点！" << endl;
            return;
        }
        G.arcs[n][m] = w;
    }
}

// 弗洛伊德算法
void MGraph::shortestPathFloyd(MGraph G, PathMatrix &P, ShortPathTable &D)
{
    // 初始化数组 P 和 D
    for (int v = 0; v < G.vexNum; v++)
    {
        for (int w = 0; w < G.vexNum; w++)
        {
            D[v][w] = G.arcs[v][w]; // D 数组元素初始值为邻接矩阵的值
            P[v][w] = -1;           // P 数组元素默认值为 -1
        }
    }

    // 拿出每个顶点作为遍历条件
    for (int k = 0; k < G.vexNum; k++)
    {
        for (int v = 0; v < G.vexNum; v++)
        {
            for (int w = 0; w < G.vexNum; w++)
            {
                // 判断经过顶点 k 的距离是否更短，若更短，则存储更短的路径
                if (D[v][k] + D[k][w] < D[v][w])
                {
                    D[v][w] = D[v][k] + D[k][w];
                    P[v][w] = k;
                }
            }
        }
    }
}

int main()
{
    MGraph G;
    G.createUDG(G); // 创建有向网

    PathMatrix P;
    ShortPathTable D;
    G.shortestPathFloyd(G, P, D); // 弗洛伊德算法

    // 打印顶点矩阵
    cout << "顶点矩阵：" << endl;
    for (int i = 0; i < G.getVexNum(); i++)
    {
        for (int j = 0; j < G.getVexNum(); j++)
        {
            cout << P[i][j] << " ";
        }
        cout << endl;
    }

    // 打印最短路径矩阵
    cout << "最短路径矩阵：" << endl;
    for (int i = 0; i < G.getVexNum(); i++)
    {
        for (int j = 0; j < G.getVexNum(); j++)
        {
            cout << D[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

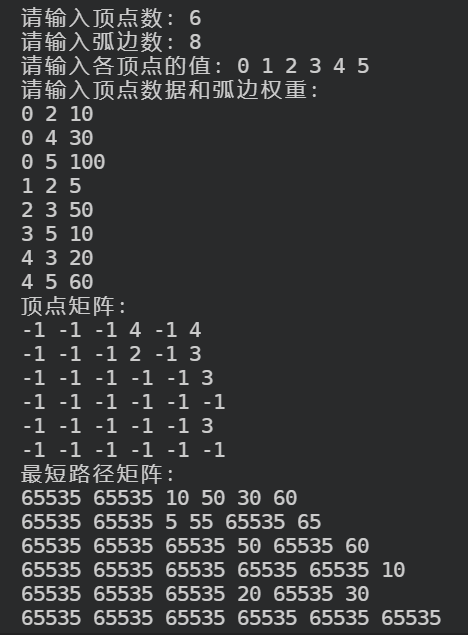
上述代码运行结果为： image20210516141033lwvmdt9.png

评论已关闭